Eular路径:Atcoder-E, Jigsaw 题解
有N块拼图碎片,每块拼图碎片都是分为三部分:左侧、中间和右侧三块,每块的宽度都是1,中间一块高度为H,左侧块高度为A,右侧块的高度为B,左侧块到底部距离是C,右侧块到底部的距离D,如下图示:
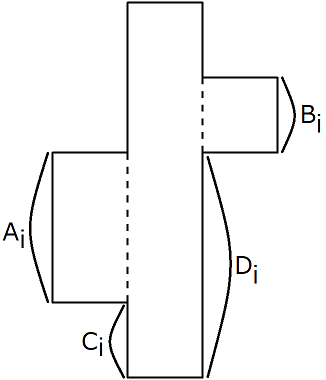
现在Alice想把这些拼图碎片拼起来放在拼图板里。拼图时要按照如下原则:
所有N块碎片必须全用上
每块拼图碎片中间一块的底部都靠在拼图板的底边上,拼图碎片不能旋转或翻转
每块碎片的左侧或右侧的块的底部必须接触拼图板底边或者接触其它拼图块右侧或左侧的顶边。
给出一组数据表示N个拼图碎片,确定这一组能否完成拼图。
第i块拼图碎片我们可以用一个(l,r)描述:
如果左侧块到底边距离C为0,则l=+A,否则l=-C
如果右侧块到底边距离D为0,则r=+B,否则r=-D
于是, (l,r)块右侧相邻的我们记为(l’,r’)。(l’,r’)能放在(l,r)的右边需要下列条件之一:
r,l’都是+(直接贴在拼图板底面上,两块不需要拼起来)
存在一个k,使r=+k时l’=-k,或者r=-k时l’=+k(两块恰好能拼起来)
同时,最左的碎片(l,r)的l必须为正,最右的碎片(l’,r’)的r’必须为负。
由此,考虑一个有2H个顶点u1,u2,…,uH,v1,v2,…,vH的有向图。
图有N条边,第i条边表示第i块碎片,l若是+k则起点为uk,若是-k则起点为vk,r若是+k则终点为vk,若是-k则终点为uk。
根据两块相邻的条件,有如下方式:
r,l’都是+的情况:最后相连的终点是v,就向某个u移动,并继续从这个点走
存在k使r=k,l’=-k的情况,从最后一条边的出边继续走
又由于最左和最右的条件,通过判定:是否可以从v到u添加多条边从而形成u到v的欧拉路径,就可以判断此问题。
#include <cstdio>
#include <cstring>
#include <vector>
using std::vector;
#define MAXN 100005
#define MAXH 405
int indeg[MAXH],outdeg[MAXH];
bool vis[MAXH];
vector<int> G[MAXH];
void add_edge(int u,int v)
{
outdeg[u]++;indeg[v]++;
G[u].push_back(v);G[v].push_back(u);
}
bool dfs(int v)
{
bool f=indeg[v]!=outdeg[v];
vis[v]=true;
for(auto to:G[v])
{
if(!vis[to])
f|=dfs(to);
}
return f;
}
int main()
{
int N,H;
int a[MAXN],b[MAXN],c[MAXN],d[MAXN];
scanf("%d%d",&N,&H);
for(int i=1;i<=N;i++)
{
scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
int l,r;
l= ( c[i]==0 ? a[i] : -c[i] );
r= ( d[i]==0 ? -b[i] : d[i] );
add_edge(l+H,r+H);
}
bool flag=true;
for(int i=0;flag && i<=H;i++)
{
if(outdeg[i]>indeg[i])
flag=false;
}
for(int i=H+1;flag && i<=2*H;i++)
{
if(indeg[i]>outdeg[i])
flag=false;
}
memset(vis,false,sizeof(vis));
for(int i=0;flag && i<=2*H;i++)
{
if((indeg[i]||outdeg[i])&&!vis[i])
flag &=dfs(i);
}
if(flag)
{
printf("YES\n");
}
else
{
printf("NO\n");
}
return 0;
}