文字列探索アルゴリズム,KMP,BM
文字列探索アルゴリズムとは?KMP法やBM法について解説 (sint.co.jp)
文字列探索アルゴリズムについて
多くのプログラミング言語において、ある文章の中に指定した文字列が含まれているかどうか、文字列検索を行うための関数やメソッドが存在します。
たとえば、Pythonのfind()関数、JavaやC#のIndexOf()メソッド、VBAのInStr()関数などがそれに該当します。
さて、これらの関数やメソッドは、どのようなアルゴリズムで文字列を探索しているか、考えてみたことはありますか?文字列探索のアルゴリズムは、なるべく早く探索を終えるための工夫がされています。それには、どのようなアルゴリズムがあるのか、また、どの程度の速さが期待されるのか、詳しく見ていくことにしましょう。
説明に当たっての前提
本記事の説明で使用する検索対象の文章は、次の通りです。
“ああいあいうあいうえあいうえお”
また、探索する文字列は、次の通りです。
“あいうえお”
文字列探索のアルゴリズムとして、以下の3つを紹介していきます。
- ナイーブ法
- KMP法
- BM法
ナイーブ法(いわゆる力任せ)
最初に、「ナイーブ法」と呼ばれるアルゴリズムについて、説明します。ナイーブ法は簡単に言うと、”力任せ”の探索アルゴリズムです。
先ほどの文章を検索する場合、次のような探索を行います。
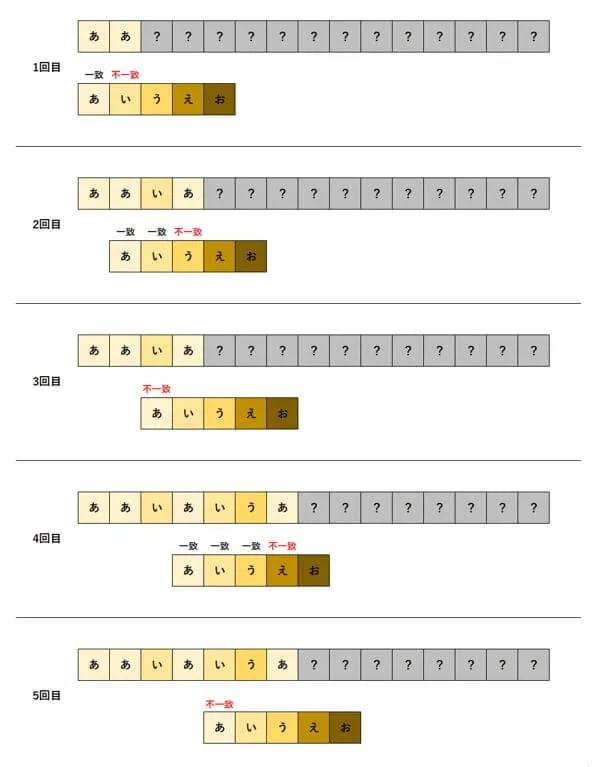
(これを繰り返す)
文章と探索文字列を先頭から1文字ずつ比較し、不一致があった場合は探索文字列を1文字だけ右に移動し、再度、探索文字列の先頭から1文字ずつ比較する、という作業を繰り返します。
大変シンプルで分かりやすいのですが、探索の速さは当然、他のアルゴリズムより劣ります。しかしながら、JavaのIndexOf()メソッドは、このナイーブ法を用いた文字列探索を行っています。
KMP法(クヌース・モリス・プラット法)
「KMP法」は、このアルゴリズムの発案者である3人(D.E.Knuth、J.H.Morris、V.R.Pratt)の名前から名付けられています。
文章と探索文字列を先頭から1文字ずつ比較するのはナイーブ法と同じですが、ナイーブ法と違う点は、探索文字列を右に移動する際の文字数です。
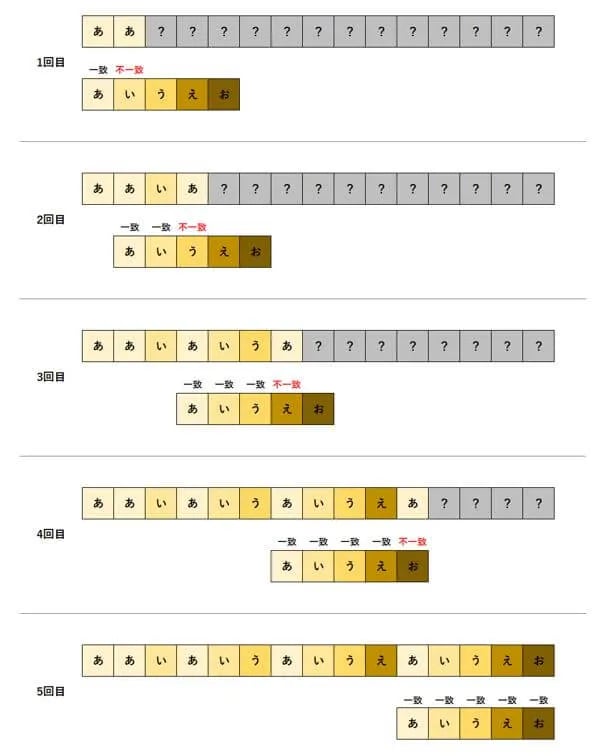
ナイーブ法は、不一致があった時点で文章を読み取る位置を右に1文字ずつ移動するのに対し、KMP法は、文章のなかに探索文字列の先頭から合致する位置を記憶することで、不要な比較を省略します。たとえば、上記のナイーブ法の説明の図における3回目や5回目の比較は、KMP法では行われません。
このような不要な比較を省略することで、ナイーブ法よりも高速な探索が期待できます。
BM法(ボイヤー・ムーア法)
「BM法」も、発案者の名前(R.S.BoyerとJ.S.Moore)から名付けられています。
BM法が、ナイーブ法やKMP法と決定的に違う点は、ナイーブ法やKMP法は探索文字列を先頭から比較するのに対し、BM法は探索文字列を後方から比較する点です。
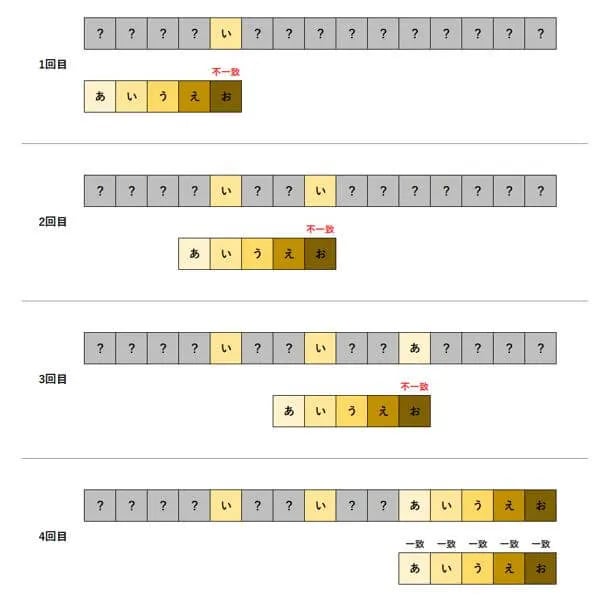
上の例の場合、1回目の比較にて、探索文字列の最後の文字と文章を比較し、不一致となりました。しかし、「い」の文字は、探索文字列の2番目の文字のため、探索文字列との比較を開始する位置を、3つ右に移動します。そこで、さらに探索文字列の最後の文字と、文章を比較します。
それぞれの速さの違いは?
それでは、紹介した3つのアルゴリズムのうち、どのアルゴリズムの探索方法が効果的か、アルゴリズムごとに期待される計算量をみてみましょう。アルゴリズムの計算量は、数学で概算を表現する際に利用されるO記法(オー記法)を用います。
計算量の算出のため、文章の文字数を「n」、探索文字列の文字数を「m」とします。
ナイーブ法の計算量
ナイーブ法の計算量は最大の場合で(最悪の場合で)、次のようになります。
O(n × m)
ここで注意したいのは、ナイーブ法の計算量は、最悪の場合でO(n × m)の比較が行われるという意味です。例えば、文章が「ああああああああああ」、探索文字列が「ああい」のようなケースが該当します。
しかし、通常、我々が日常的に使用する自然言語のなかで、このように同じ文字が何度も続くケースは稀です。そのため、ナイーブ法の実質的な計算量は、O(n)に近い値になります。具体的には次のようなケースをイメージしてみてください。文章が「ああああああ桜餅食べたい」、探索文字列が「桜餅」の場合。
KMP法の計算量
KMP法の計算量は、次の通りです。基本的には探索文字列に対して、重複した無駄なく1周分探すようなイメージでしょうか。また、KMP法は最良の場合でも最悪の場合でも計算量に大きな変化がないのが特徴です。
O(n)
BM法の計算量
最後に、BM法の計算量は「最良の場合」に次のようになります。
O(n / m)
ただし、これは最良の場合です。ナイーブ法で紹介した最悪の場合と同じく、文章と探索文字列のなかに同じ文字が多く含まれている場合、文章と探索文字列の比較を何度も行うことになり、結果として、計算量はO(n × m)まで落ちてしまう可能性があります。ただ、そんなケースは稀ですので、日常的にある文章に対して、文字列検索をする場合には、BM法が最速の手法であると言ってもよさそうです。
まとめ
文字列探索のアルゴリズムについて、ナイーブ法、KMP法、BM法の3種類を紹介しましたが、いかがでしたか?
計算量の比較では、BM法がもっとも計算量が少なく、高速であるという結果となりました。しかし、前述のとおり、JavaのIndexOf()メソッドは、ナイーブ法を用いています。なぜでしょうか?
ナイーブ法は、探索文字列の文字数が少ない(「n」の値が小さい)ときは、KMP法やBM法の計算量との違いが小さくなります。たとえば探索文字列が1文字の場合は、計算量はナイーブ法、KMP法、BM法で同じ結果となります。
また、Javaの場合、正規表現(文字列の集合をパターン化して表現する技法)を使えるため、探索文字列のパターンが複雑な場合は正規表現を用いることの方が多く、また、現代のコンピューターの処理速度は、よほど多くの文字列を探索しない限りは、目に見えて処理速度に影響を与えることは、あまりないのかも知れません。
ちなみに、文字列探索のアルゴリズムは、IPA主催の情報処理技術者試験のアルゴリズムの問題として出題されることもあります。情報処理技術者試験を受験する予定の方はもちろん、そうでない方もITスキルを磨くための一つのステップとして、各アルゴリズムの名称や概要を覚えておくとよいと思いますよ。